电机技术与原理

电磁场

在电能到机械能的转换过程中，起关键作用的是磁场。磁场可以由电流产生，也可以由永磁体产生。磁性材料包括永磁材料和软磁材料，是电机实现能量转换的关键部件。 一方面，硅钢等软磁材料可以在较低的励磁电流下得到较大的磁通密度，从而提高能量密度，而高性能永磁材料可以在不施加励磁电流的情况下得到稳定的磁场，有利于实现更高的电机效率；另一方面，磁性材料的应用可以限制和规范磁通流经的路径，利用这一特性，可以通过适当的设计来优化电机特性，尤其是扭矩。

安培定律

电流产生磁场，即电励磁的基本定律——安培定律，又称安培环路定理。载流导线会产生磁场，而载流导线所载有的电流与磁场沿着闭合回路的路径积分之间的关系为：

\[\int \vec{H} \cdot dl = \sum I\]

H是由回路所包围的净电流∑i所产生的磁场强度，dl是沿着积分路径的微分元。在国际单位制中磁场强度H的单位是安培每米（A/m）。电流方向和其产生的磁场方向之间的关系服从右手定则。

对电机的应用来说，电励磁主要是电流环绕铁芯的情形，在这种情况下铁磁材料的独特物理性质会给电机及其他磁性器件的设计带来极大的便利。

导线绕在磁性铁芯（如硅钢等）的一侧，电流从左上方流入，从左下方导线内流出。不同于在空气中或者真空中的情形，由于这些铁芯具有较高的磁导率，类似于电流在导线中流动但不会穿过导线表面而流入空气中一样，图中电流产生的磁场会主要局限在铁芯中。这样在计算铁芯中的磁场时，安培定律中的积分路径就是铁芯的平均长度lC，假定电流线圈的匝数是N，则积分路径内的净电流就是Ni，所以：

\[Hl_C = Ni\]

磁动势

磁场强度H可以被认为是外界为激励磁场所做的努力，而Ni又被定义为磁动势，通常用F代表，类似于电场中的电动势或者电压。

磁通

磁场的施加会在铁芯中产生磁通，磁通密度B依赖于磁场强度以及铁芯的磁性特征，它们之间的关系可以描述为：

\[B = \mu H = \mu_0 \mu_r H\]

这里B是磁通密度，是单位面积上的磁通量，单位是Wb/m2。μ0称为真空磁导率，是个常数，4π×10-7T·m/A，而μr为相对磁导率，依赖于介质，在空气或者真空中为1，而对于电机中常用的电工钢，根据工况的不同，其数值可以很大，在2000～80000之间。相对磁导率的大小反映出磁性材料对于外磁场的响应，而这种比较高的相对磁导率的好处是显而易见的。

从上述公式中可以看出，相比于在空气中，在相同磁场下的铁磁性材料或介质中产生的磁通密度高几千甚至上万倍。所以在电机、变压器以及别的磁性器件中，磁性铁芯是一个重要部件，它可以提高和汇聚磁通。

穿过一个表面（比如图中的铁芯截面）的磁通总量，称为磁通量，是磁通密度对截面积的积分：

\[\Phi = \int_A B \cdot dA\]

电流除了能产生磁场之外，根据法拉第电磁感应定律（Faraday’s Law of Induction），当通过一个线圈的磁通发生变化时，线圈中将会产生感应电动势。感应电动势的大小取决于磁通随时间的变化速率：

\[e_{ind} = -N \frac{d\Phi}{dt}\]

感应电动势和磁通变化率的关系式中的负号，是因为感应电动势的产生会阻止磁通的变化。确定感应电动势方向的物理定律称为楞次定律。

法拉第定律是变压器运行的基本定律，同时也是分析电机性能的重要定律。相邻两个线圈，当其中一个线圈中的电流发生变化时，引起周围磁场的变化，其邻近线圈中会产生感应电动势，称为互感。在同一线圈内部，当电流发生变化时会产生感应电动势，以阻碍导体中电流的变化，称为自感。在电机中，感应电动势分为两种，一种是导体在磁场中运动，或者导体和磁场有相对运动时所产生的电动势，称为动生电动势；而另外一种是由于交流电流的变化引起的磁通量的变化，称为感生电动势。

磁阻

磁路是在设计与分析磁性器件时的一个十分有用的工具。通过和电路类比，磁路及其相关概念和分析方法的引入会更加容易理解。在上节的讨论中，我们已经提到磁动势类似于电路中的电动势、电压，而磁通等同于电路中的电流，磁通密度等同于电流密度。

对比电压电流关系式，不难看出，与电阻对应的是lc/(μA)，即磁阻。这样，电路和磁路分析就完全对应起来了。

\[\Phi = B \cdot A = \frac{\mu Ni A}{l_C} = \frac{Ni}{\frac{l_C}{\mu A}}\]

磁通的流向由右手定则决定，即取决于导线中电流的流向以及导线的环绕走向。同样类似于电路中的情形，在磁路中不同磁阻的组合下，如串联、并联，总磁阻的计算按照与电路分析中同样的规则。不同的是，在电路中，导线电导率和空气及别的绝缘介质的电导率的差异可以达到10的10次方量级，甚至更高，所以在电路分析中，电流基本完全局限在回路中。在磁路中则不然，空气和常用软磁材料电工钢之间的磁导率的差异与工况有关，即便在最高磁导率下，也只有约10的6次方量级，所以忽略漏磁是一个比较粗略的近似。在很多情况下磁路分析是为了简化问题、便于分析的一个工具，但是基于磁路的定量计算并不能给出准确的结果。

驱动电机中的磁性材料

磁性材料，准确地说是铁磁性材料，是电机的关键组件。电机中用的磁性材料有两种，软磁材料和永磁材料。

软磁材料：放大磁信号，规范和引导磁通。 永磁材料：本身一经磁化就可以产生稳定持续的磁场，而无须消耗额外的能量，跟电励磁相比，无须电流。

铁磁性材料最本质的特性是自发磁化和磁畴。自发磁化是指物质在无外加磁场的情况下，原子间的相互作用使原子磁矩自发地形成在空间内有序的排列。对于铁磁性材料来说原子磁矩会形成平行排列而具有较大的宏观磁矩M，从而呈现宏观磁性。

但是通常在无外加磁场或者磁化（未曾暴露在外磁场中）之前，铁磁性材料本身并不显示出磁性。原因就是在材料内部形成了很多很小的磁化均匀的区域，称为磁畴，这些小区域内部的磁化是均匀的、一致的，但是不同的小区域之间磁化成不同的角度，整体呈随机排列，因而相互抵消不显示出宏观磁性。

在外加磁场的作用下，每个磁畴的磁化方向开始逐渐与外加磁场相一致，逐渐趋向平行排列的不同磁畴的磁矩开始显示累加效应，并叠加到外场上，于是就有了远远大于真空磁导率μ0的磁导率μ=μrμ0，又称为有效磁导率。

随着磁场的增加，这种趋势会持续下去，直到所有的磁矩均与外场平行，总磁矩达到最大值，磁体达到饱和状态。当外磁场逐渐撤去，这种磁化状态并不能保持。在无外磁场的状态下，磁化方向会回到由材料的晶体结构对称性决定的易磁化轴方向。

所以，磁化后的磁铁在外磁场逐渐移去后，并不回到初始的完全退磁的状态，而是会保留一部分净磁矩，这种现象称为磁滞。

由于磁滞现象的存在，磁场强度H和磁通密度B之间的关系并非线性的、单值的，而是高度依赖于磁铁在磁场中被磁化的历史。这种依赖性可以通过磁铁在外磁场作用下磁通密度的变化即BH回线来表示。BH曲线同时是表征磁性材料的最常用曲线。

B-H曲线，磁化曲线

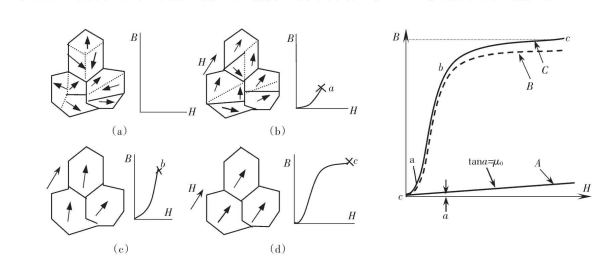
将完全无磁状态的铁磁物质放在磁场中，磁场强度从零逐渐增加，测量铁磁物质的磁通密度B，得到磁通密度和磁场强度H之间关系，并用B-H曲线表示，该曲线称为磁化曲线，如下图所示。

没有磁化的磁介质中的磁畴完全是杂乱无章的，所以对外界不表现磁性（a）。当磁介质置于磁场中，外磁场较弱时，随着磁场强度的与外磁场方向相差不大的那部分磁畴逐渐转向外磁场方向（b），磁感应B随外磁场增加而增加（oa段）。如果将外磁场H逐渐减少到0时，B仍能沿ao回到0，即磁畴发生了“弹性”转动，故这一段磁化是可逆的。当H继续增大时，B急骤增加，几乎成直线上升（ab段），当H进一步增大时，B的增加又变得缓慢，达到c点以后，H值即使再增加，B却几乎不再增加，即达到了饱和。

右图下方的曲线是空气中磁通密度的变化，与上方曲线对比也可以看出铁磁材料对于磁通密度的增强作用。

驱动电机中的能量转换

在电机中，能量转换可以分为两种情形，一种是电流或通电导线在磁场中的情形，而另外一种则是没有电流的情形。带电粒子在纯磁场中的运动受到的力称为洛沦兹力，对于点电荷而言：

\[\vec{F} = q(\vec{v} \times \vec{B})\]

其中，q是粒子电荷，v是粒子速度。所以带电粒子受到的力取决于电荷的大小、运行速度以及磁场强度。洛伦兹力的方向既垂直于粒子运动方向又垂直于磁场方向，因为它是二者的矢量积，因而可以用左手定则来确定其方向，即将左手掌摊平，让磁力线穿过手掌心，四指表示正电荷运动方向，则和四指垂直的大拇指所指方向即为洛伦兹力的方向。

在实际应用中，更多的情形不是单个粒子在磁场中运动，而是大量电荷或者电流在磁场中运动。由于i是电流强度，磁场中的导线长度是l，因而其大小为：

\[F = i l B \sin \theta\]

θ是导线中电流方向和磁场方向的夹角。

如果导线线圈暴露在磁场中，如下图所示，虚线所示是线圈的中心，中心到导线的距离是r，则在磁场作用下在上下导线中产生的力沿着线圈平面方向的分量会产生力矩F·r驱动线圈转动，这就是直流电机的工作原理。很明显，要使导电线圈转动起来，电流方向需要不停地切换，因此直流电机需要电刷和换向器等附加部件。